Proportional reasoning is a foundational skill in culinary math, enabling chefs and kitchen staff to maintain consistency, control costs, and scale recipes efficiently. In a professional kitchen, where precision and profitability are paramount, understanding and applying proportional reasoning is not just an academic exercise—it’s a daily necessity.

Discussion: Conceptual understanding of proportional reasoning based on student experience

Understanding Proportional Reasoning

Proportional reasoning involves recognizing the relationship between quantities and understanding how changing one quantity affects another. In the context of culinary math, this could mean adjusting a recipe for a different number of servings, converting ingredient measurements, or ensuring that the cost of ingredients aligns with the budget.

A ratio is a comparison between two quantities, such as the amount of flour to water in a bread recipe. A proportion is an equation that states that two ratios are equal. For example, if a recipe requires a 2:1 ratio of flour to water, and you double the flour to 4 cups, you must also double the water to 2 cups to maintain the proportion.

Key terms:

• Ratio: A comparison between two quantities.
• Proportion: An equation that states two ratios are equal.
• Scaling: Adjusting the quantities of ingredients in a recipe to produce a different yield.
• Yield: The total amount produced by a recipe.
• Costing: The process of calculating the cost of ingredients and the total cost of a recipe or dish.

A proportion is a statement that two ratios or fractions are equal. For example, if you know that a recipe requires 2 cups of flour to make 12 cookies, and you need to make 24 cookies, proportional reasoning allows you to determine that you’ll need 4 cups of flour.

Mathematically, this can be expressed as:

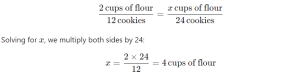
This simple example illustrates the power of proportional reasoning in the kitchen, but its applications go far beyond scaling recipes.

Importance of Proportional Reasoning in Costing Food

Costing food accurately is critical to the success of any food service operation. Proportional reasoning plays a central role in this process, ensuring that ingredients are used efficiently and that the final cost of a dish aligns with the pricing strategy.

1. Recipe Scaling and Cost Adjustments: When scaling a recipe up or down, it’s crucial to adjust the ingredient quantities proportionally. If a chef needs to make a larger batch of a dish, the cost of the ingredients will increase accordingly. By applying proportional reasoning, chefs can estimate the total cost based on the scaled quantities, ensuring that they stay within budget.

For instance, if a dish costs $5 to make 4 servings, scaling up to 8 servings should theoretically cost $10. However, ingredients are not always linear in cost (bulk purchases might reduce per-unit costs), so proportional reasoning also helps in recognizing and adjusting for these variations.

1. Yield Management: In professional kitchens, not all purchased ingredients are used entirely, and the yield (the usable amount after preparation) must be accounted for. Proportional reasoning helps in calculating the cost of the usable portion of an ingredient. For example, if a 10-pound fish costs $30, but only 7 pounds are usable after cleaning, the cost per pound of usable fish is higher than the original purchase price. This adjustment is essential for accurate food costing.
2. Menu Pricing: Setting menu prices involves understanding the cost of ingredients and ensuring that each dish is profitable. Proportional reasoning aids in breaking down the cost per portion and determining the appropriate markup to meet financial targets. For example, if the total cost of a dish is $8 and the desired food cost percentage is 30%, proportional reasoning helps in setting the menu price at approximately $26.67.
3. Portion Control: Consistent portion sizes are vital for maintaining cost control and customer satisfaction. Proportional reasoning ensures that each portion uses the correct amount of ingredients, minimizing waste and ensuring that each dish’s cost remains consistent.

Practical Applications in the Kitchen

In a fast-paced professional kitchen, chefs regularly use proportional reasoning to make quick decisions. Whether adjusting a sauce for a different number of servings, modifying a recipe based on available ingredients, or recalculating costs when ingredient prices change, proportional reasoning is a versatile tool.

For example, imagine a scenario where a chef has planned to make a batch of soup for 100 guests, but an additional 25 guests are unexpectedly added. Using proportional reasoning, the chef can quickly determine the new quantity of each ingredient needed and the adjusted cost, ensuring that there’s enough food without overspending on unnecessary ingredients.

Moreover, proportional reasoning helps chefs make substitutions or adjustments to recipes without compromising quality or flavor. If an ingredient is unavailable or too expensive, the chef can use proportional reasoning to determine how much of a substitute ingredient is needed to maintain the dish’s integrity.

Original Recipe (Serves 10):

• Chocolate: 200 grams
• Heavy Cream: 400 milliliters
• Egg Whites: 4
• Sugar: 80 grams

Scenario:

A catering event requires enough chocolate mousse to serve 60 guests. The chef needs to scale the recipe while maintaining the same taste, texture, and quality.

Applying Proportional Reasoning:

To scale the recipe from 10 to 60 servings, the chef needs to multiply each ingredient by a factor of 6, since 60 servings is six times the original 10 servings.

By using proportional reasoning, the chef ensures that all ingredients are scaled evenly, preserving the balance of flavors and textures. This method guarantees that the mousse will taste the same as the original, whether it’s made for 10 or 60 people. Additionally, the chef can accurately calculate the total cost of ingredients for the larger batch, ensuring that the pricing for the event is consistent and profitable.

This example highlights the importance of proportional reasoning in scaling recipes, which is crucial for maintaining consistency and efficiency in a professional kitchen.

Conclusion

Proportional reasoning is more than just a mathematical concept; it’s a practical skill that underpins many aspects of professional cooking. From scaling recipes to controlling costs, chefs rely on proportional reasoning to ensure that their kitchens run efficiently and profitably. By mastering this skill, culinary professionals can make informed decisions that contribute to both the success of their dishes and the financial health of their operations.